Topics:

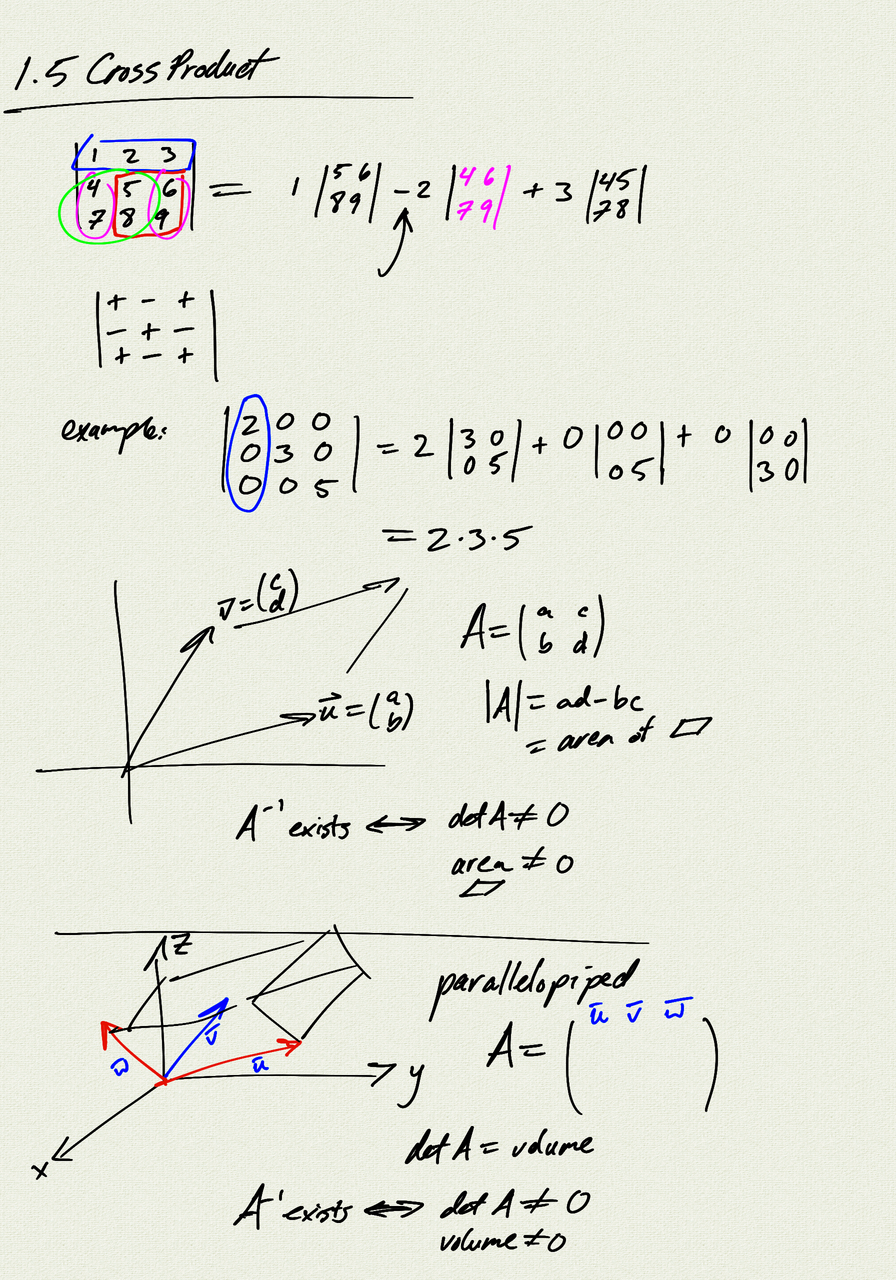
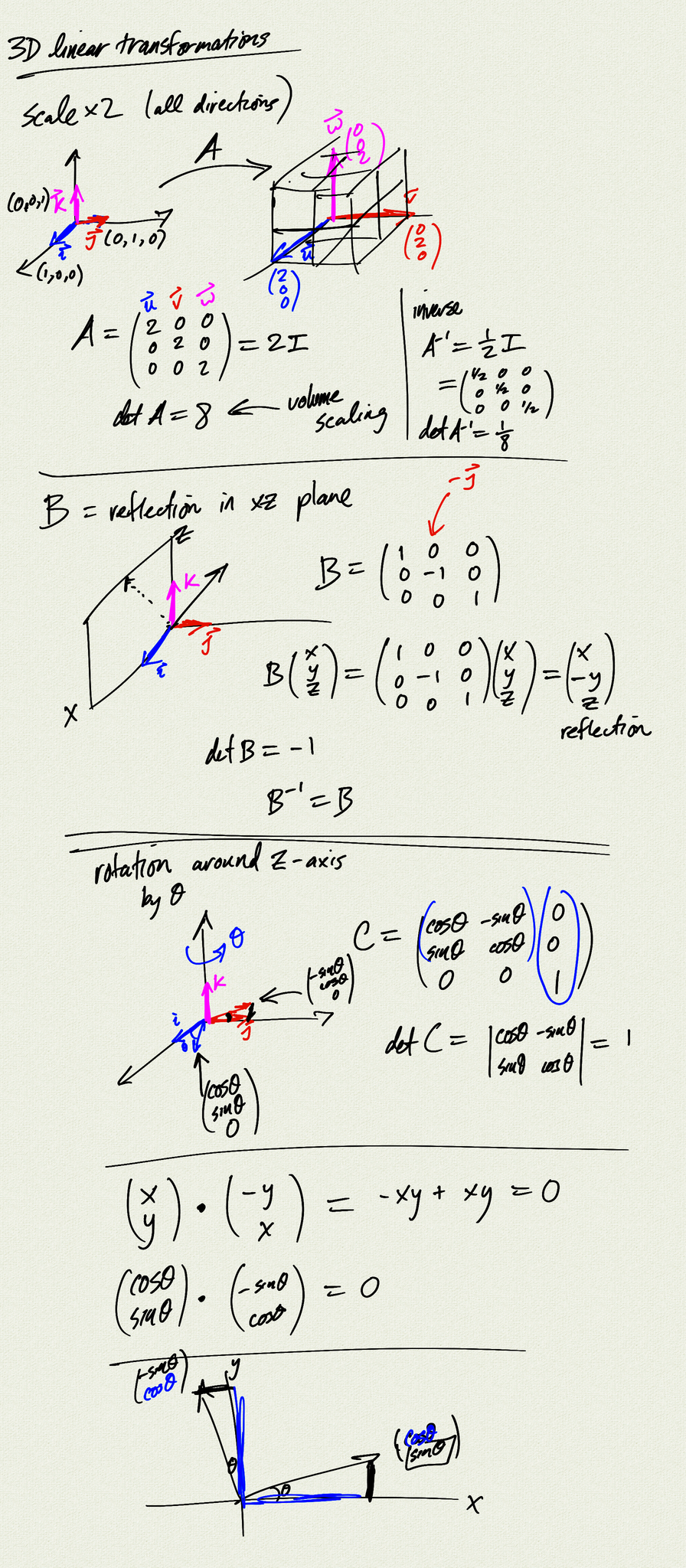
  • linear transformations in $\mathbb{R}^3$
    • determinant and volume
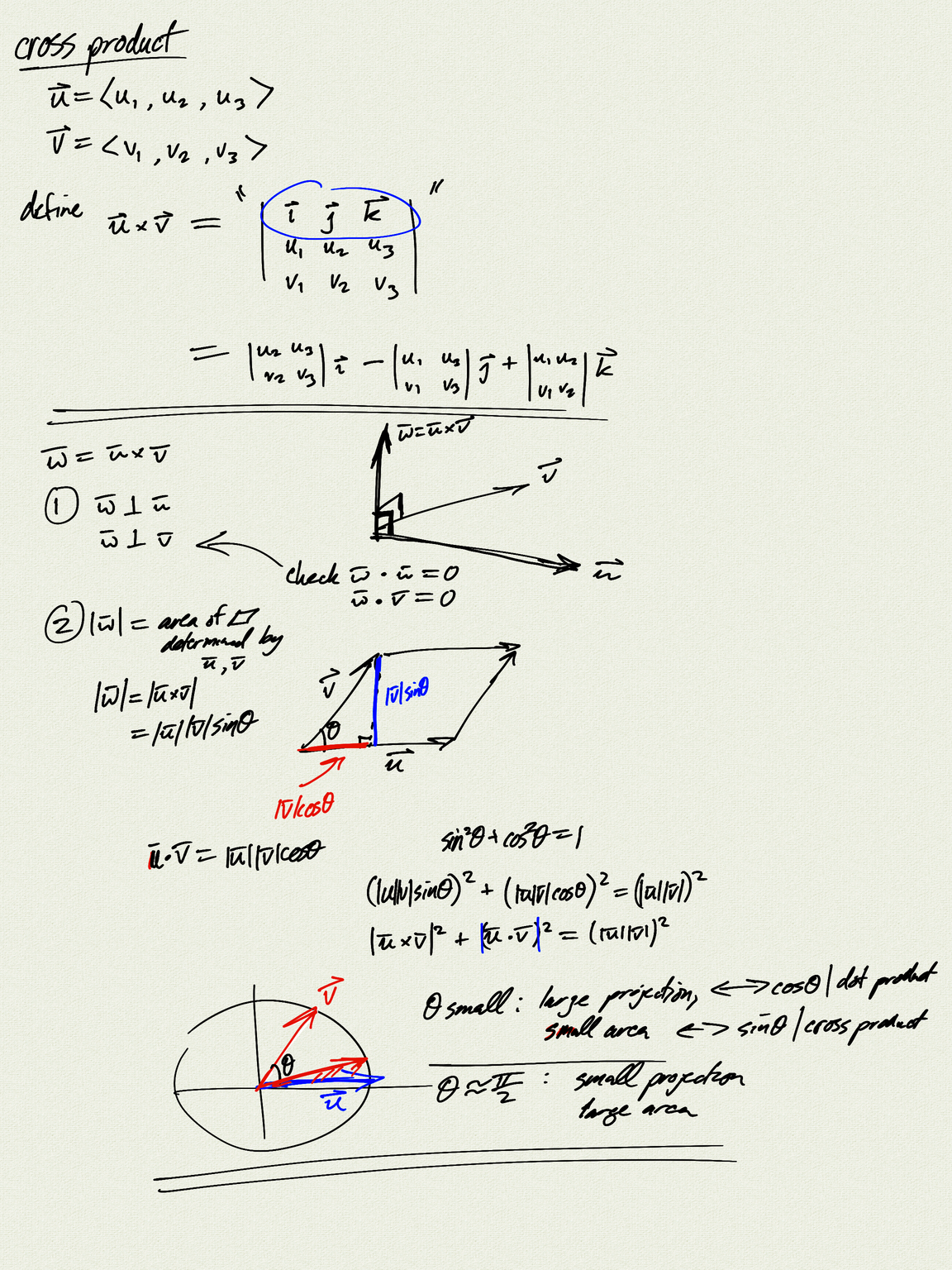
  • cross product $\vec{w} = \vec{u} \times \vec{v}$
    • $\vec{w}$ is orthogonal to $\vec{u}$ and $\vec{v}$
    • $|\vec{w}|$ = $|\vec{u}||\vec{v}|\sin\theta$ = area of parallelogram
    • right hand rule
  • scalar triple product
  • $ |\vec{u} \cdot \vec{v}|^2 + |\vec{u} \times \vec{v}|^2 = |\vec{u}|^2 |\vec{v}|^2 $

Reference: OSC 2.4 Cross Product

notes (pdf)